Torsion [Part 2]
In the previous post we examined the model of two cantilevers and came up to that constraining of warping can significantly change the deformations and stresses.
Let’s continue the same experiment with another, third cantilever.
I want to achieve the state of stresses and deformations similar to the right cantilever, but without “cheating”, with something real, that can be produced in real life. Yes, absolute rigid bodies are imaginable, they don’t exist in real life unfortunately.
So the first try — transverse ribs on the free end of cantilever.
Can these ribs work as a rigid element?
Will they prevent the end section from warping?
No. Absolutely not. The warping of the beam hasn’t even noticed their existence here.
But why?..
It’s easy.
This rib is just a steel plate that is relatively thin and it subjected to be bended out of its plane.
It has really small stiffness in this case, right?
Simple transverse ribs don’t help I-beams with torsion.
But what can help?
Maybe more ribs?
A little, but not enough.
And five pairs of ribs for cantilever of only four meters long is already too many.
Let search for somethin effective.
But before we get to the answer, I want to make a lyrical digression.
closed sections
It looks like magic. Two models on the left are so “untwistable” so you may ask if I forgot to even apply any load there. But the load on all these 5 models are the same. And not only loads.
Will you be surprised if I tell you that even the sections are almost the same?
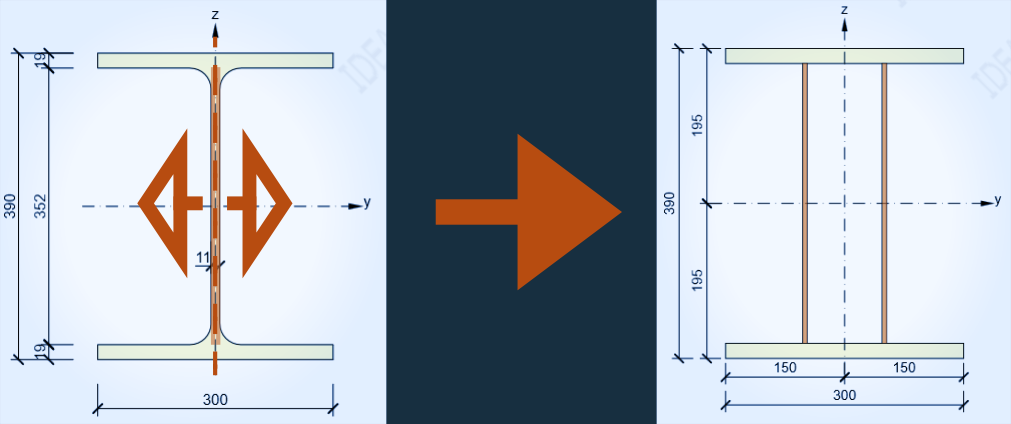
I have taken the original section and created the same one with only one difference. The thin web was divided into two even thinner webs, which were spread apart a little.
The original web has thickness of 11 mm, two new webs — 5.5 mm each with 100 mm distance between them.
And it changed everything! This deep purple color shows us almost zero stresses. The deformations, comparing to I-sectioned beams, are… absent?
New section has the torsional constant (I.t) of 20+ times higher, which makes St Venants stresses much much lower. The stresses from magnitudes of 150..200 MPa lowered to … 6..8 MPa.
Okay, what about warping here? “Negligible” for closed sections, say books. To understand this negligibility, I want you to guess what is the difference between two models on the left. Like we did in the beginning of Torsion [Part 1] post.
Yes, the answer is still the same. One of them has the rigid element on its end. But if for open section that rigid element changed picture completely, for closed section it has done completely nothing.
Okay, reveal the magic
I don’t believe it is possible to show this effect better than they did on this picture in
SCI Guide P385.
Look at these pictures and imagine how these small arrows can unite to some kind of pairs of forces to resist external moment.
For open sections they have no synergy for it. It is just a lot of very small counter-moments spread along the section.
For closed section it is really a team work!
Make it stand out
Whatever it is, the way you tell your story online can make all the difference.
For our section we can show these internal shear stresses the same way.
And even if we cut away the parts outside of the “box”, the torsional constrain will lower only by 3%!
The section after cutting off more than 60 percent of its flanges still resists torsion with quite no effort!
Okay, closed sections are for torsion. Understood. But…
Yes, let’s return to the main question of this post — how to “stiffen” the open section exposed to torsion.
Let's try different approaches on the same cantilever. AM1 and AM2 are "control models" — one with nothing on its end, other with absolute restriction for warping.
We will be trying to apply different potential solutions to see which one would be closer to AM2 and further from AM1.
Okay, we had already tried the transverse rib and that attempt failed. How about… longitudinal ribs?
Or even better — both transverse ribs on the end AND longitudinal ribs
And, to check all the options related, the full-box option — two pairs of transverse ribs and longitudinal ribs also.
I can already hear the curses of fabricator for the amount of operations needed to perform this.
Looks like we have one definite winner and two accomplished losers.
Yes, the only option of these three that actually worked — it is the “full box” option.
But why?
Let’s have a closer look at how the beam flanges deform at the free end.
These flanges are bending in horizontal directions, in opposite directions. They are like twisting around the vertical axis, right? But now we know what is the best way to prevent any torsion. And this is closed section.
And our “rib box” created a vertical tube (closed section!) that prevents their rotation relative to each other:
So, this is the answer.
Stiffener that can restrict torsion deformations must have a closed section.
To prove this statement, the last demonstration for today:
Here we have 5 types of stiffeners
Two angles (L-section), forming a square box.
<>A tube, placed instead of portion of the cantilever's web — the solution that once showed me my friend Andrey Golenkin ;)
OTwo channels (U-section). Here we have two sub-options:
[ ] — closed
] [ — openAlready known for us box of longitudinal and transverse ribs
▯
Almost all of these stiffeners did their work properly. Almost. But one — that one that hasn’t created any “tube” as a stiffener.
In the next episodes
Bimoment — what does it mean?
What is 7th degree of freedom?
What is interesting about channels?
Torsion stiffness in IDEA StatiCa connection
…
Subscribe to this blog and to my LinkedIn page and don’t miss the next post!
STILL HAVE QUESTIONS?
Torsion is not the most well-known topic about structural design. But there are a lot of interesting topics and a lot of possibilities to apply IDEA StatiCa.
If want to deepen your knowledge or want to get acquainted with the program, consider joining one of our comprehensive IDEA StatiCa courses.
Explore our courses to find the one that suits your needs best or request a custom course.
Get in touch with us today to learn more or to sign up!