Torsion [Part 3]
Recap
What have we discussed in two previous posts?
St Venant torsion relates to shear stresses, while warping torsion involves shear and direct stresses.
Closed sections offer significant benefits for torsion.
When warping is limited, torsion deformations are reduced.
The element can resist warping on its own, without the need for external supports.
Today, I want to discuss the significance of boundary conditions and how torsion is implemented in 1D elements in FEM software.
But first, let's address some common questions that engineers frequently ask themself.
Bimoment
Warping torsion causes direct stresses. The stresses in each beam flange may be combined to form a bending moment, which bends the flange within its own plane.
For a symmetrical beam subjected to torsion these moments in two flanges are equal and opposite in direction as it shown on the picture. This moment in each flange is called warping moment.
Bimoment is just a product of warping moment magnitude on a distance between flanges centers.
Like a… moment of a moment. The kN×m×m.
Channel section
The U-beams bend in the interesting way. It is usual to think, that torsion appears out of nowhere for such beams, and that torsion appears for them always.
But this is not particularly true.
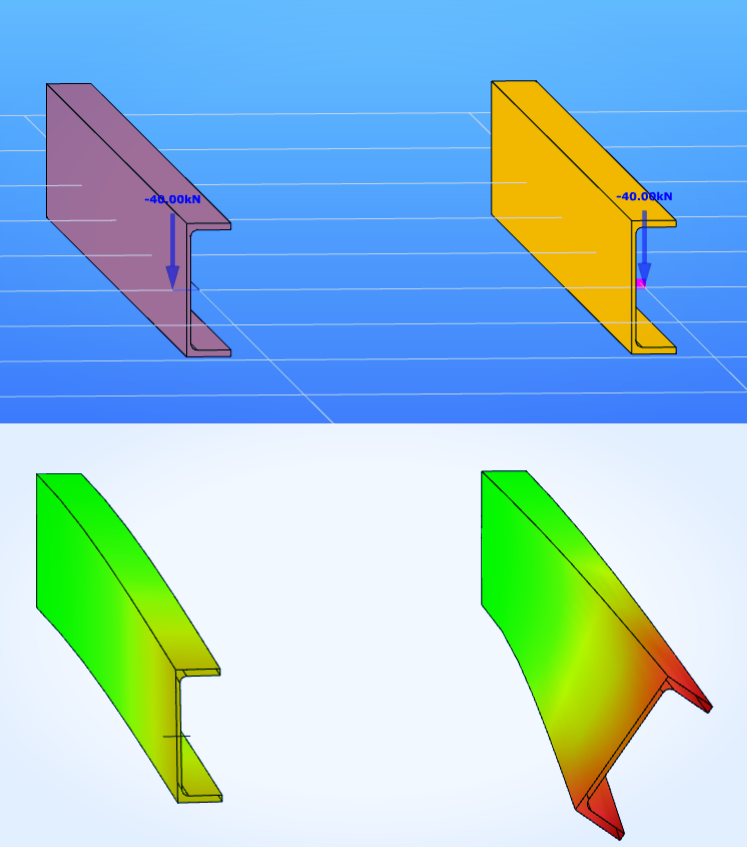
Picture shows a channel cantilever with applied vertical load on its end in channels center of gravity. Colors show the magnitude of total deformations.
Where did this torque come from?
I don’t want to explain the whole concept of the shear center here, all you need to know now — that if you want the beam not to twist — apply load exactly there.
Any load out of this point — it is eccentric load that makes a beam to twist.
So when we load the U-beam on the center of gravity or within the web plane — all of it should be considered as eccentrical load with applied torsional moment.
So when the load is placed to the shear center, channel-sectioned cantilever bends “vertically”.
Commercial break
For every blog post I create a batch of different CBFEM models, that allow me to illustrate these or that effects or laws of structural mechanics. Thanks to IDEA StatiCa I can create, calculate and analyze them withing a few minutes! And you can do it too! Feel free to contact me and arrange a course to master your knowledge!
IDEA StatiCa Courses
🟧
IDEA StatiCa Courses 🟧
Let’s compare results to FEM-software
I mean software that you usually use for overall structural calculations, where beams are modelled with 1D-elements (bar elements).
Today some software started to implement so-called “7dof” (7th degree of freedom) for their bar elements. It means that such bars have ability to calculate internal warping moment and therefore the bimoment.
Today I used trial version of Consteel to perform some simple tests.
First of all — comparison with the example above
No surprises, everything works as it should — the load to the center of gravity of the section rotates the cantilever, to the shear center — only bends.
Reminder: This shows a visual representation of the bar elements model, not a model of shell elements.
Boundary conditions
In classical 6-degree-of-freedom approach we have six directions for boundary conditions of a node — Ux, Uy, Uz, Rx, Ry, Rz (these terms have different names in various software, but I refer to U as the symbol for translational deformations and R for rotational deformations here).
When FEM-software allows you to implement 7th DOF, both bar model and border conditions receives the update. Let’s have a look.
Upper image is from IDEA StatiCa Member, lower —bar model in Consteel
Here are two similar structural models. Model in IDEA StatiCa Member is obviously more complex — all six beams have different boundary conditions — different random connections, different columns orientation.
First, the results in IDEA StatiCa Member, total deformations are shown on the picture:
Of course, the difference lies in the connections. Let’s take a closer look on them with the context of the results above.
Six random connection designs that are not intended for any specific loads, and some are practically impossible to install.
Simple fin-plated joint with low rotational stiffness and practically zero warping stiffness (nothing prevents the end section from warping). The result — highest deformations of the beam center.
End-plate connection that is usually considered as simple, or at least semi-rigid. The columns web has no ribs, so I would say that the warping constraint is minimal.
Cleat connection. The warping constraint here is even lower and the rotational displacements of the beam are therefore bigger.
The most rigid connection. Rigid for bending moment and for torsion. And with really high warping stiffness — ribs in the column with thick end-plate. As a result — the lowest rotation of the center of the beam — around 2.5 times lower than for connection 1.
Totally the same connection as 1, but with the warping constraining element (vertical RHS tube) near the connection.
Surprisingly, isn’t it? The most flexible option (1) became more rigid than the number 4.The same connection as in option 2, but the flexible thin column web is changed to absolutely rigid element. This example shows that not only the column web was guilt of warping, but also the connection itself.
The conclusion that we can draw here is that the warping constraints are indeed significant for elements that are subjected to torsion.
How to implement it in FEM Software?
Consteel dialogue of releasing any of seven degrees of freedom
Obviously, it is only possible for software that implements 7dof elements. Such a software gives user a possibility to release the end of a bar in this 7th way or to set the magnitude for warping stiffness.
Here in the picture you can see how it works in Consteel.
How to determine this value of the warping stiffness?
The fly in the ointment here is that I have never heard of any universal approaches of how to measure such a warping boundary stiffness.
Dlubal has some tool for certain cases and they refer to some German book, but… aber ich kann kein Deutsch lesen.
What is “stiff” in terms of warping and torsion?
The other issue — no structural code or standard will give you any boundary values for “rotationally rigid” joints or something.
You can measure the bending stiffness of a connection using IDEA StatiCa Connection or the Eurocode's component method and classify it as rigid or hinged. However, you cannot do this for torsional stiffness.
So… Engineering judgement? Experiments?
Yes, exactly! Look at the picture below. It is the same 1d-bar-model in Consteel, but looks pretty close to IDEA StatiCa’s result, isn’t it?
Three left beams have warping releases on their ends and three others have not.
If we compare each with corresponding result from IDEA StatiCa Member we will see that results are more or less close.
To refine results more we can calculate precise torsional stiffnesses in IDEA StatiCa Connection and apply them to Consteel as partial releases.
Stresses
Stresses of a beam in torsion consists of shear stresses from St Venant torsion and mostly direct stresses from warping torsion. For an I-beam, the highest warping stresses occur at the flange edges, while shear St. Venant stresses are not presented at this points.
P385 on the page 20 says that it is enough to calculate only warping stresses for I-beam.
Results of 1d-bar-model calculation in Consteel. Bimoments in sections (not the stresses)
Warping stresses from bimoments
The equivalent stresses in IDEA StatiCa for beams 1-3 lies in interval of 206…212 MPa, and this result is very closed to 214 MPa of stresses, obtained from bimoments on 7dof model.
Models 4 and 5 with well-constrained warping showed stresses level of 160-168 MPa. Which is 10-15% lower than stresses, calculated from bimoments.
Nice results for 1d finite element, aren’t them?
Conslusion
I had no aim to compare results or verify something. The more I wished to give some tips of how the IDEA StatiCa Member and Connection may help you to make more or less accurate assumptions to use them in global analysis with implemented seven degrees of freedom.
Also, I hope I’ve demonstrated the purpose of this seventh degree at all. And the significant role of design of connections on the ends of a beam to the stresses in the middle of it.
The final advice will be — don’t subject your structural elements to torsion until it is really needed. Choose another structural solution if possible. Especially if the element has open section. But if you have to do it — I hope you now have some information on how to handle the torsion.
I’ll be waiting for your feedback after these three huge posts — here in comments, on LinkedIn page, in my email inbox or even by sms.
STILL HAVE QUESTIONS?
Torsion is not the most well-known topic about structural design. But there are a lot of interesting topics and a lot of possibilities to apply IDEA StatiCa.
If want to deepen your knowledge or want to get acquainted with the program, consider joining one of our comprehensive IDEA StatiCa courses.
Explore our courses to find the one that suits your needs best or request a custom course.
Get in touch with us today to learn more or to sign up!